以轮换 2 为中心展开的相关内容探讨

在许多领域中，我们常常会遇到与轮换相关的情况。而这里，我们将重点围绕“轮换 2”展开深入的探讨。

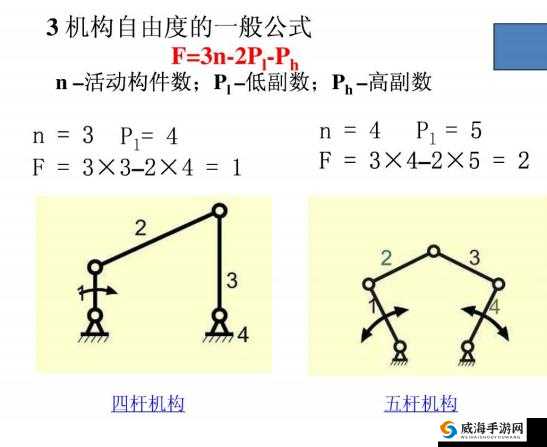
让我们来明确一下轮换的概念。轮换可以被理解为按照一定顺序依次替换或交换元素的操作。而当我们聚焦在“轮换 2”时，意味着每次只涉及两个元素的交换。

在数学中，轮换 2 有着广泛的应用。例如在排列组合问题中，通过对特定元素进行轮换 2 的操作，可以帮助我们分析和解决各种计数问题。考虑一个简单的例子，给定一组数字，通过不断进行两个数字的轮换，可以产生不同的排列组合，从而深入理解概率和统计中的相关概念。

在计算机科学领域，轮换 2 也能发挥重要作用。在算法设计中，可能需要对数据进行特定的交换操作，以实现某种特定的功能或优化。比如在排序算法中，通过巧妙地运用轮换 2 的策略，可以逐步将数据调整到有序状态。

从日常生活的角度来看，我们也能找到与轮换 2 相关的情景。比如在人员的工作安排中，通过定期进行两人之间的轮换，可以确保公平性和多样性，避免某些人长期承担特定任务而产生疲劳或不公平感。在团队协作中，轮换 2 可以促进成员之间的交流与合作，使每个人都能体验不同的角色和任务，从而提升团队的整体效率和凝聚力。

在艺术创作中，轮换 2 也能带来新奇的效果。比如在音乐创作中，通过对两个音符或两个节奏模式进行轮换，可以创造出独特的旋律和韵律。在绘画中，色彩或元素的轮换可以营造出不同的视觉效果和情感氛围。

以轮换 2 为中心也并非没有挑战。在实际操作中，需要仔细考虑轮换的时机、顺序和频率，以避免不必要的混乱或负面影响。如果轮换过于频繁或不恰当，可能会导致系统的不稳定或效率下降。

在确定轮换 2 策略时，还需要充分考虑到相关因素的影响。比如在团队中进行人员轮换时，要考虑到每个人的技能和能力，确保轮换不会影响工作的正常进行。在算法中运用轮换 2 时，要权衡计算复杂度和效果之间的关系。

“以轮换 2 为中心展开的相关内容探讨”揭示了轮换 2 在各个领域的重要性和多样性。通过深入理解和合理应用轮换 2 的概念，我们可以在数学、计算机科学、日常生活和艺术等诸多方面取得更好的效果和体验。但我们也要谨慎对待其可能带来的挑战，通过精心的规划和管理，使轮换 2 真正为我们的学习、工作和生活带来积极的影响。随着对轮换 2 研究的不断深入，相信它将在更多的领域展现出其独特的价值和魅力。

以上文章仅供参考，你可以根据实际情况进行调整和补充，希望能帮助到你！